MCRA Memorial Hall

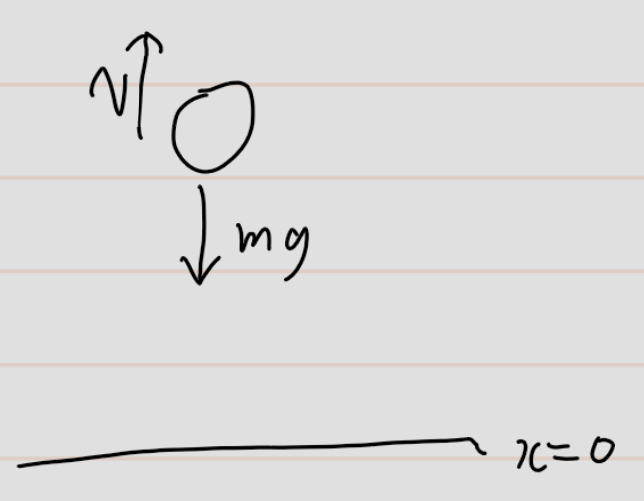
자유낙하왼쪽그림은 중력을 받으면서 위로 올라가는 그림F = -mg = (-dV \over dx) 이고, E = (\frac{mv^2}{2} + mgx)E = (\frac{mv_0^2}{2} = \frac{mv^2}{2} +mgx)(v^2 = v_0^2 -2gx)최고점에 다다르먼 v=0 이 된다. 즉 (x_{max} = \frac{v_0^2}{2g})  ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ중력가속도F는 -G(\frac{mM}{r^2})이렇게 정의된다. 여기서 지구표면에서 중력가속도가 대략 9.81 인걸 증명해보자면 F = ma = -G(\frac{mM}{r^2}) -> a = -G(\frac{M_{지구무게}}{r_{지구반지름}})= 대략 9.81여기서 G =중력상수이다. 지구표면이 아닌 지구 밖에서 중력가속도 g' --..

직각 좌표계 xyz가 있고, x'y'z'좌표계는 x축기준으로 , y축기준으로 , z축기준으로 (\theta) 만큼 회전했을때 변환행렬을 알아보자.기존 xyz좌표계에서 x성분을 (\hat{i}) , y성분을 (\hat{j}) , z성분을 (\hat{k})라 하고, x'y'z'좌표계에서 x'성분을 (\hat{x'}) , y'성분을 (\hat{j'}) , z'성분을 (\hat{z'}) 이라하자. 행렬을 이용해 위 그림들을 표현해보면 x'y'z'을 가지는 벡터를 A'이라 하고 xyz를 가지는 벡터를 A라 하면(\begin{pmatrix} A'_x \\ A'_y \\ A'_z \end{pmatrix})  = (\begin{pmatrix} \hat{i} \cdot \hat{i'} & \hat{j} \cdot \ha..

구면거울의 공식 증명 (\frac{1}{P} + \frac{1}{i} = \frac{1}{f} = \frac{2}{r}) 우선 그림을 그려보면이고 여기서 (\alpha + \theta + (180 - \beta)) = 180  => (\alpha + \theta = \beta) 인 걸 알 수 있다. 그리고 같은 원리로 (\beta + \theta + (180 - \gamma) => (\beta + \theta = \gamma) 이다.밑에식과 위에식 빼주면 (\alpha + \gamma = 2\beta) 가 된다.여기서 각도들이 전부다 매우작다고 가정하면 (\theta = \sin \theta = \tan \theta)이므로 (\tan \alpha + \tan \gamma = 2\tan \beta) 가 되..

전자기파 (E = E_msin(kx-wt)) , (B = B_m sin(kx-wt)) 이렇게 나타낼수 있다.그리고 맥스웰 4가지 법칙중에 페러데이 법칙에 의해(\oint E \cdot ds = \frac{d\Phi_B}{dt}) 임을 알수있고,그림에서 볼수 있듯이 전기장 E를 선적분을 하면 1번에서 전기장이 y성분으로 움직이니 (\int_{a}^{b} \vec{E} d\vec{y} = (E+dE))h2번에서는 -x방향으로 전기장 성분이 없으니 0이다.3번에서는 -y성분으로 가니 (\int_{c}^{d} \vec{E} d\vec{y} = -Eh)4번에는 +x방향으로 전기장 성분이 없으니 0이다.즉 1+2+3+4 = (dEh)이다. 즉 (\oint E \cdot ds = \frac{d\Phi_B}{dt} =..

우선 어떤 컵 안쪽으로 음파가 발생한다 치자. 그럴때 음파가 고체,액체,기체를 통과하는 파동이 되서 압력차가 생긴다. 이때 압력차 (\triangle p) = (-\beta * \frac{\triangle V}{V}) ((\beta : 부피 탄성률 , V = 부피 )) 이 공식은 증명하기에 일반물리학수준에서 딱히 필요하지도 않고 시간낭비다. 그러나 고체물리할때 아는게 좋을거 같으니 고체물리하기전에는 증명하는게 좋다.어쨋든 (\triangle p) = (-\beta * \frac{A\partial s}{A\partial x})여기서 변위 s = (s_mcos(kx-wt)) 이렇게 표현해보자(진동은 사인코사인 아무거나 사용해서 표현해도 된다.결국 위상차만 바뀌는거니깐 딱히 상관없음) 어쨋든 s를 x에대해 미..

우선 먼저 파동에는 여러가지 종류가 있지만 할리데이 일반물리학에서는 간단하게 가로파동과 세로파동만 알면된다. 가로파동은 예를들어 설명하자면 줄을 흔들었을때 파동의 진행방향과 파동의 움직이는 방향은 수직한다는걸 알수있다. 세로파동은 음파같이 파동의 진행방향이 파동의 운동방향과 나란할때 이다. 이번 16장에서는 가로파동에 대해서 공부할 것 이다.파동함수에는 여러가지가 있지만 사인형 파동부터 보자.여기서 (y = Asin(kx-kvt))를 보면 sin속 안에 값들은 단위가 '라디안'이나 '도' 여야한다. 즉 kv를 w로 정의해줘서(y =Asin(kx-wt)) 이렇게 변형이 가능하다. 그럼 여기서 (v = \frac{w}{k})를 알 수 있다. 그리고 v = (\lambda) / T ((\lambda) : 파장..

2단원에서는 질량보존법칙,일정성분비법칙,배수비례법칙 이 세가지가 수학에서 공리처럼 화학에서 아주 기본이되는 법칙이기에 꼭꼭 알아야된다. 우선 화학에서 질량보존법칙은 화학반응전 질량과 화학반응 후 질량은 똑같다. 즉 반응전 질량 = 반응후 질량 이 말이다. 일정성분비법칙은 어떤 화합물은 항상 질량기준 같은 비율의 원소를 가진다는것을 의미힌다. 예를들어 H2O는 H - 2g , O - 16g 이다. 여기서 수소 1g은 무조건 산소 8g이랑 1:8로 반응해야만한다. 배수비례법칙은 화합물이 첫번째 원소1g와 결합하는 두번째 원소의 질량 비율은 항상 정수비로 증감한다. 예를들어 CO 와 CO2를 보자. CO에서 산소는 16/44 만큼 있다. CO2에서 산소는 32/44 만큼있다. 즉 16/44 : 32/44 = ..

1단원에서 중요하고 꼭 기억했으면 하는거는 제목 그대로 유효숫자 규칙들과 완전수, 불완전수 이다. 연역법 이란 가설을 먼저 세우고 실험을 반복적으로 하여 결과를 도출한다. 귀납법은 실험을 먼저 반복하고 그 실험속에서 가설을 찾고 결론을 도출한다. 유효숫자는 아래 규칙을 꼭 기억하자 1. 0이 아닌 정수는 모조리 유효숫자 갯수에 포함시킨다. 2. 0이 아닌 정수 앞에 오는 0은 유효숫자 갯수에 포함 시키지 않는다. ex) 0.0002 - 1개 3. 0이 아닌 정수들 중간에 오는 0은 포함 시킨다. ex)1.008 - 4개 4. 0이 아닌 정수들 오른쪽에 오는 0은 소수점이 없을때 포함 시키지 않는다. ex) 200 - 1개 5. 0이 아닌 정수들 오른쪽에 오는 0이 소수점이 있다면 포함시킨다. ex) 20..

지금까지 본 우크라이나 전쟁에서 정말 인상적이라 생각하는 것은 드론이다. 넓은 전장에서 드론으로 쉽게 공격,정찰,방어 등등 모든 곳에서 드론이 나타난다.위 사진은 우크라이나가 전선에 납품하는 FPV 카미카제 드론들이다. 드론들도 여러가지 종류가 있다. 일반적으로 쿼드콥터 드론을 많이 이용한다. 왜냐하면 비용 효율성도 좋고, 접근성,민첩성,안정성,유지관리 면에서 압도적으로 좋기 때문이다. 또 쿼드콥터 공격 드론에서도 직접 타격 드론과 정찰용 일반 드론에 수류탄을 매달아 떨어뜨리는 Grenade-dropping drone 이 두가지 드론들을 많이 사용한다. 쿼드콥터드론 외에도 지상자폭드론,수중자폭드론 등등 우크라이나군이 많이 사용한다.우선 위 gif에 나온 직접 타격 드론은 높은 정확도와 좀 더 즉각적인 공..